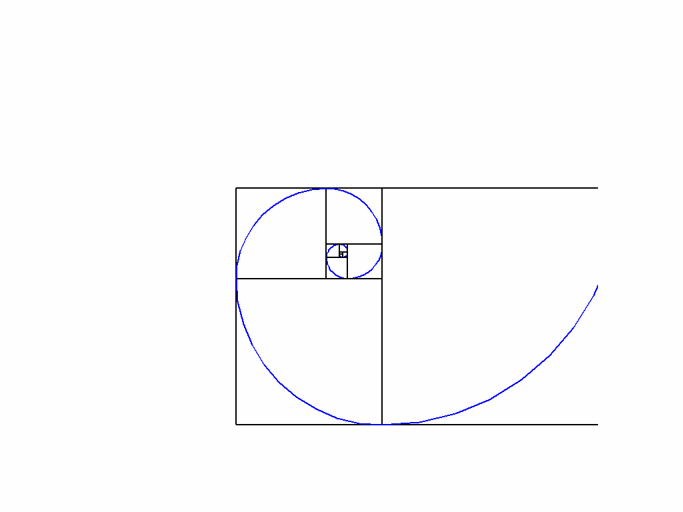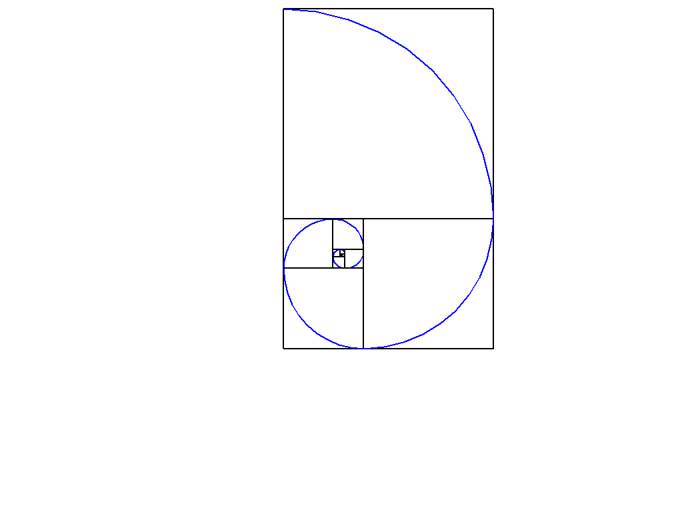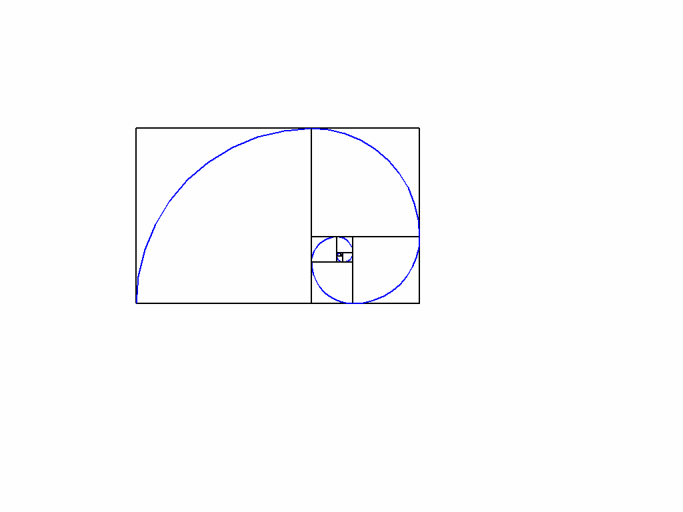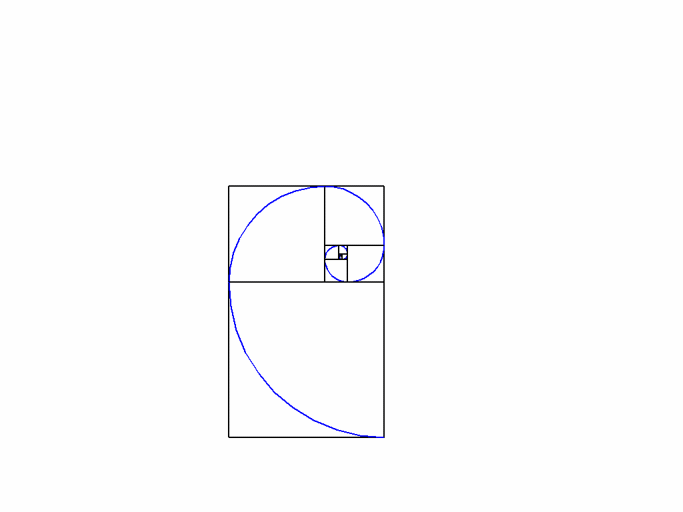
✅ La suite de Fibonacci converge vers le nombre d’or. Chaque ratio entre termes consécutifs tend vers 1,618, illustrant l’harmonie mathématique.
La relation entre la suite de Fibonacci et le nombre d’or est fascinante et se manifeste de plusieurs manières. La suite de Fibonacci est une série de nombres où chaque nombre est la somme des deux précédents, généralement débutant par 0 et 1. Les premiers termes sont donc 0, 1, 1, 2, 3, 5, 8, 13, etc. Le nombre d’or, souvent noté par la lettre grecque phi (φ), est approximativement égal à 1,6180339887… Ce nombre apparaît naturellement dans diverses disciplines, notamment l’art, l’architecture et la nature.
Nous allons explorer en détail cette relation entre la suite de Fibonacci et le nombre d’or. Nous allons d’abord examiner comment les rapports entre les termes successifs de la suite de Fibonacci se rapprochent du nombre d’or. Ensuite, nous aborderons les implications de cette relation dans différents domaines. Nous présenterons également des exemples concrets et des illustrations pour mettre en lumière cette connexion mathématique profonde.
La suite de Fibonacci et ses rapports
En observant les termes de la suite de Fibonacci, nous pouvons calculer les rapports entre chaque paire de termes successifs. Par exemple :
- 1/1 = 1
- 2/1 = 2
- 3/2 = 1,5
- 5/3 ≈ 1,6667
- 8/5 = 1,6
- 13/8 ≈ 1,625
En continuant cette série, on constate que ces rapports commencent à converger vers le nombre d’or (φ). Plus nous avançons dans la suite, plus le rapport entre deux termes successifs se rapproche de 1,618. Ce phénomène est un exemple de la propriété de convergence des suites numériques et illustre comment le nombre d’or est profondément enraciné dans la structure mathématique des nombres.
Applications du nombre d’or et de la suite de Fibonacci
La relation entre la suite de Fibonacci et le nombre d’or dépasse la simple théorie mathématique. Voici quelques exemples d’applications :
- Architecture : De nombreux bâtiments célèbres, comme le Parthénon en Grèce, utilisent le nombre d’or dans leur conception pour créer des proportions esthétiquement plaisantes.
- Nature : On retrouve des motifs basés sur la suite de Fibonacci dans la disposition des feuilles sur une tige, la spirale des coquillages et même dans la disposition des graines dans un tournesol.
- Art : Des artistes tels que Léonard de Vinci et Salvador Dalí ont intégré le nombre d’or dans leurs œuvres, croyant qu’il s’agissait d’une expression de la beauté divine.
Illustration de la relation
Pour illustrer visuellement cette relation, on peut tracer un rectangle d’or dont les dimensions respectent le ratio du nombre d’or. En divisant ce rectangle en carrés, on peut dessiner une spirale qui représente la suite de Fibonacci. Cette spirale apparaît dans de nombreux éléments naturels, ce qui renforce l’idée que la mathématique et la nature sont intimement liées.
Applications pratiques de la suite de Fibonacci et du nombre d’or
La suite de Fibonacci et le nombre d’or ne se limitent pas à des concepts mathématiques abstraits ; ils ont des applications concrètes dans divers domaines. Analysons quelques-unes des utilisations les plus fascinantes et les plus utiles de ces deux concepts.
1. Arts et design
Dans le monde de l’art et du design, le nombre d’or est souvent utilisé pour créer des compositions harmonieuses. Par exemple :
- Peinture : Des artistes comme Leonard de Vinci ont utilisé le nombre d’or pour structurer leurs œuvres, ce qui leur confère une beauté esthétique.
- Architecture : Des bâtiments célèbres, tels que le Parthénon en Grèce, intègrent cette proportion pour un équilibre visuel parfait.
2. Nature et biologie
La suite de Fibonacci apparaît fréquemment dans la nature. Voici quelques exemples :
- Phyllotaxie : La disposition des feuilles sur une tige suit souvent la suite de Fibonacci, permettant une meilleure exposition au soleil.
- Fleurs : Le nombre de pétales de nombreuses fleurs, comme les lys (3 pétales) ou les chrysanthèmes (21 pétales), correspond aux nombres de Fibonacci.
3. Informatique et algorithmes
Dans le domaine de l’informatique, la suite de Fibonacci est utilisée dans le développement d’algorithmes. Par exemple :
- Les algorithmes de recherche et de tri peuvent être optimisés en utilisant la suite de Fibonacci, ce qui rend les opérations plus efficaces.
- Les structures de données comme les arbres de Fibonacci sont utilisées pour créer des files d’attente prioritaires, ce qui améliore la gestion de la mémoire.
4. Finance
Un autre domaine où la suite de Fibonacci et le nombre d’or jouent un rôle crucial est la finance. Les analystes boursiers utilisent souvent les niveaux de retracement de Fibonacci pour prédire les tendances des marchés. Par exemple :
- Les investisseurs peuvent identifier les points de support et de résistance sur les graphiques des prix, en se basant sur des ratios dérivés de la suite de Fibonacci.
- Ces niveaux aident à prendre des décisions d’achat ou de vente basées sur des mouvements de marché historiques.
Tableau récapitulatif des applications
| Domaines | Applications |
|---|---|
| Arts et design | Composition harmonieuse, architecture |
| Nature et biologie | Phyllotaxie, nombre de pétales |
| Informatique | Algorithmes optimisés, structures de données |
| Finance | Niveaux de retracement, décisions d’investissement |
Ces applications pratiques montrent que la suite de Fibonacci et le nombre d’or ne sont pas simplement des curiosités mathématiques, mais des outils puissants que l’on peut utiliser dans de nombreux aspects de notre quotidien.
L’histoire et l’origine de la suite de Fibonacci et du nombre d’or
La suite de Fibonacci trouve ses racines dans un ouvrage du mathématicien italien Leonardo de Pise, connu sous le nom de Fibonacci, publié en 1202 intitulé “Liber Abaci”. Dans ce livre, Fibonacci présente une série de nombres qui commence par 0 et 1, où chaque nombre suivant est la somme des deux précédents. Ainsi, les premiers termes de la suite sont :
- 0
- 1
- 1
- 2
- 3
- 5
- 8
- 13
- 21
- 34
Ce concept de la suite de Fibonacci a d’abord été introduit pour modéliser la croissance des populations de lapins, mais il a depuis évolué et trouve des applications dans divers domaines, tels que la biologie, l’art, la musique et même l’architecture.
Le nombre d’or : une beauté mathématique
Le nombre d’or, souvent symbolisé par la lettre grecque phi (φ), est un nombre irrationnel approximativement égal à 1,6180339887. Sa signification réside dans sa présence dans la nature et dans la composition esthétique. Le rapport entre deux segments de droite est dit être en nombre d’or lorsque le rapport du plus grand au plus petit segment est le même que le rapport de la somme des deux segments au plus grand segment.
Il existe une relation fascinante entre la suite de Fibonacci et le nombre d’or. À mesure que l’on avance dans la suite de Fibonacci, le rapport entre deux termes successifs tend vers le nombre d’or :
- 1/1 = 1,0
- 2/1 = 2,0
- 3/2 = 1,5
- 5/3 = 1,666…
- 8/5 = 1,6
- 13/8 = 1,625
- 21/13 = 1,615384615…
- 34/21 = 1,619047619…
Il est intéressant de noter que cette convergence vers phi se produit à mesure que les termes de la suite augmentent, ce qui a fasciné les mathématiciens pendant des siècles.
Cas d’utilisation
Les applications du nombre d’or et de la suite de Fibonacci se retrouvent dans :
- Architecture: Utilisé pour concevoir des bâtiments esthétiquement plaisants, comme le Parthénon.
- Art: De nombreux artistes, dont Leonardo da Vinci, ont appliqué ce principe dans leurs œuvres.
- Nature: Les spirales de coquillages et les phyllotaxies des plantes sont souvent en relation avec la suite de Fibonacci.
En somme, l’histoire de ces concepts mathématiques est un fascinant mélange de nature, de beauté et de logique, marquant leur place dans notre monde à travers les âges.
Questions fréquemment posées
Qu’est-ce que la suite de Fibonacci ?
La suite de Fibonacci est une série de nombres où chaque nombre est la somme des deux précédents. Elle commence généralement par 0 et 1, donnant ainsi la séquence 0, 1, 1, 2, 3, 5, 8, etc.
Qu’est-ce que le nombre d’or ?
Le nombre d’or, noté φ (phi), est une proportion irrationnelle d’environ 1,6180339887. Il est souvent trouvé dans la nature, l’art et l’architecture, représentant une harmonie esthétique.
Comment la suite de Fibonacci est-elle liée au nombre d’or ?
À mesure que l’on avance dans la suite de Fibonacci, le ratio entre deux nombres consécutifs converge vers le nombre d’or. Plus les nombres sont grands, plus le rapport se rapproche de φ.
Où trouve-t-on le nombre d’or dans la nature ?
Le nombre d’or peut être observé dans des formations naturelles comme les spirales de coquillages, les arrangements de feuilles sur une tige, et même dans la façon dont les galaxies se forment.
Comment utiliser la suite de Fibonacci en design ?
La suite de Fibonacci peut être appliquée pour créer des compositions équilibrées et harmonieuses, notamment dans le design graphique et l’architecture, en utilisant le nombre d’or comme guide proportionnel.
Points clés de la relation entre la suite de Fibonacci et le nombre d’or
| Concept | Description |
|---|---|
| Suite de Fibonacci | Série de nombres où chaque terme est la somme des deux précédents. |
| Nombre d’or (φ) | Proportion d’environ 1,618, considérée comme esthétiquement plaisante. |
| Convergence | Les ratios de nombres consécutifs de Fibonacci se rapprochent de φ. |
| Applications | Utilisé en art, architecture, et design pour créer des compositions harmonieuses. |
| Nature | Présent dans des structures naturelles comme les spirales et les arrangements floraux. |
Nous aimerions connaître votre avis ! Laissez vos commentaires ci-dessous et n’oubliez pas de consulter d’autres articles sur notre site qui pourraient également vous intéresser.