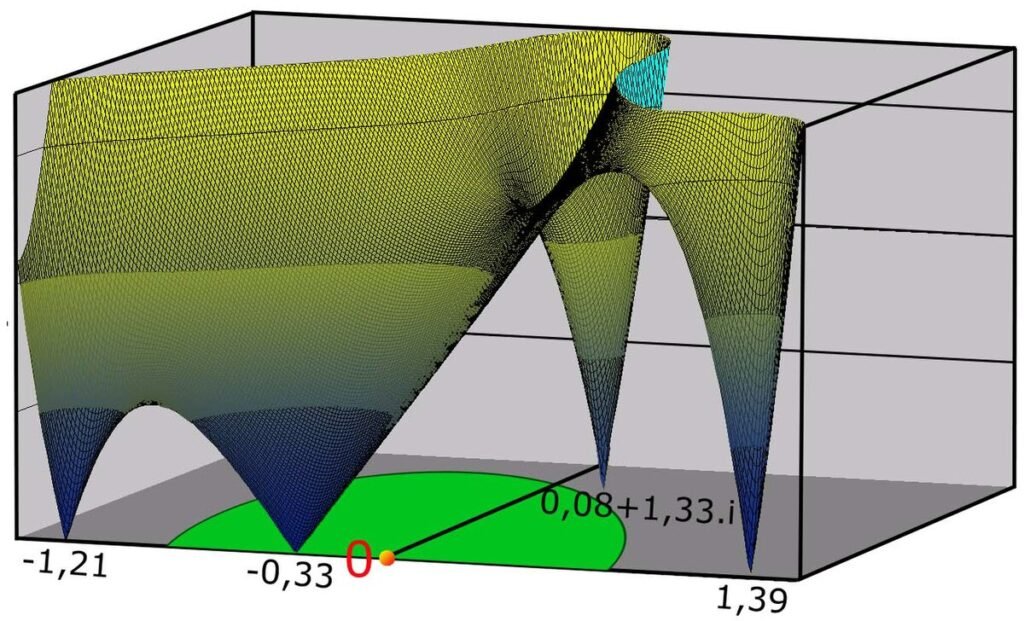
✅ Utilisez des méthodes numériques comme l’algorithme de Newton-Raphson ou l’optimisation pour résoudre efficacement des systèmes non linéaires.
Pour résoudre un système d’équations non linéaires efficacement, il est essentiel de choisir la méthode appropriée en fonction de la complexité du système. Parmi les techniques les plus courantes, on trouve la méthode de Newton, la méthode de substitution, et la méthode graphique. Chacune de ces méthodes peut être adaptée à des situations spécifiques afin d’atteindre une solution optimale.
Présentation des méthodes de résolution
Nous allons explorer en détail trois méthodes principales pour résoudre un système d’équations non linéaires. La méthode de Newton est souvent utilisée pour sa rapidité et son efficacité lorsque les équations sont suffisamment différentiables. La méthode de substitution, quant à elle, est plus intuitive et peut être plus facile à appliquer pour des systèmes simples. Enfin, la méthode graphique permet d’avoir une visualisation des solutions, bien qu’elle soit moins précise pour des systèmes complexes.
1. Méthode de Newton
La méthode de Newton est une méthode itérative qui utilise les dérivées des fonctions pour converger vers une solution. Elle est particulièrement efficace pour des systèmes avec plusieurs variables. Voici un aperçu des étapes de cette méthode :
- Initialisation : Choisissez un point de départ proche de la solution.
- Calcul : Évaluez les fonctions et leurs dérivées.
- Itération : Mettez à jour le point selon la formule de mise à jour de Newton.
- Convergence : Répétez jusqu’à ce que la solution converge.
2. Méthode de substitution
La méthode de substitution consiste à exprimer une variable en fonction des autres et à substituer cette expression dans les autres équations. C’est une méthode simple et efficace pour des systèmes de petites dimensions. Voici les étapes :
- Isoler une variable dans l’une des équations.
- Substituer cette variable dans les autres équations.
- Répéter jusqu’à avoir une équation en une seule variable.
- Résoudre cette équation pour obtenir la valeur de la variable.
3. Méthode graphique
La méthode graphique consiste à tracer les courbes des équations sur un graphique et à identifier les points d’intersection. Bien qu’elle soit moins précise, elle est utile pour obtenir une première idée des solutions d’un système.
Pour tracer les équations, suivez ces étapes :
- Réécrire chaque équation sous forme explicite si nécessaire.
- Tracer chaque fonction sur le même graphique.
- Identifier visuellement les points d’intersection qui représentent les solutions du système.
Conseils pour une résolution efficace
Pour maximiser l’efficacité dans la résolution de systèmes d’équations non linéaires, voici quelques conseils pratiques :
- Utilisez des outils logiciels comme MATLAB ou Python pour effectuer des calculs complexes.
- Vérifiez la présence de solutions multiples ou des solutions complexes.
- Privilégiez la méthode graphique pour une compréhension visuelle des systèmes simples.
- Testez différentes méthodes pour voir celle qui converge le plus rapidement.
Techniques numériques pour la résolution des équations non linéaires
Les équations non linéaires peuvent souvent être difficiles à résoudre analytiquement, ce qui rend les techniques numériques indispensables. Ces méthodes permettent d’obtenir des solutions approximatives avec un degré de précision suffisant pour diverses applications pratiques. Nous allons explorer quelques-unes des techniques les plus courantes.
Méthode de Newton-Raphson
La méthode de Newton-Raphson est l’une des techniques les plus populaires pour résoudre les équations non linéaires. Elle utilise une approche itérative pour trouver les racines d’une fonction. Voici les étapes principales :
- Choisir une valeur initiale proche de la solution.
- Calculer l’itération suivante à l’aide de la formule : x_{n+1} = x_n – frac{f(x_n)}{f'(x_n)}.
- Répéter jusqu’à ce que la différence entre les itérations soit suffisamment petite.
Par exemple, pour résoudre l’équation x^2 – 2 = 0, on peut commencer avec une valeur initiale de x_0 = 1.5 et appliquer la méthode pour converger vers la racine √2.
La méthode de bisection
La méthode de bisection est une approche simple et robuste qui repose sur le théorème du Bolzano. Cette méthode est basée sur le principe que si une fonction change de signe entre deux points, il existe une racine dans cet intervalle. Voici comment elle fonctionne :
- Déterminer deux points, a et b, tels que f(a) cdot f(b) < 0.
- Calculer le point médian c = (a + b) / 2.
- Vérifier le signe de f(c) pour déterminer dans quel sous-intervalle se trouve la racine.
- Répéter jusqu’à obtenir une précision désirée.
Cette méthode est particulièrement utile lorsque la dérivée de la fonction est difficile à calculer.
La méthode de la fausse position
La méthode de la fausse position (ou méthode de Regula Falsi) est similaire à la méthode de bisection, mais elle utilise une approximation linéaire pour améliorer la convergence. Voici les étapes :
- Choisir deux points a et b avec f(a) cdot f(b) < 0.
- Calculer le point d’intersection de la droite reliant les points (a, f(a)) et (b, f(b)) avec l’axe des x :
c = b – frac{f(b) cdot (b – a)}{f(b) – f(a)}. - Mettre à jour a ou b selon le signe de f(c) et répéter.
Ce processus permet souvent d’atteindre des résultats avec moins d’itérations que la méthode de bisection.
Tableau comparatif des méthodes
| Méthode | Convergence | Complexité | Exigences |
|---|---|---|---|
| Newton-Raphson | Rapide (quadratique) | O(1) par itération | Dérivée nécessaire |
| Bisection | Lente (linéaire) | O(log(n)) | Changement de signe |
| Fausse position | Modérée | O(log(n)) | Changement de signe |
En choisissant la méthode appropriée, il est crucial de prendre en compte les caractéristiques de la fonction à résoudre ainsi que la précision souhaitée. Par exemple, la méthode de Newton-Raphson est très efficace pour des fonctions bien comportées, tandis que la méthode de bisection est plus fiable pour des cas où la continuité et le changement de signe sont garantis.
Logiciels et outils pour simplifier la résolution des systèmes non linéaires
Dans le monde mathématique moderne, plusieurs outils et logiciels sont à disposition pour faciliter la résolution des systèmes d’équations non linéaires. Ces outils offrent des méthodes et des algorithmes avancés qui permettent d’économiser du temps et d’améliorer l’efficacité des calculs. Voici quelques-uns des plus populaires :
1. MATLAB
MATLAB est un logiciel puissant pour le calcul numérique. Il propose la fonction fsolve pour résoudre des systèmes d’équations non linéaires. Un exemple d’utilisation est :
fsolve(@(x) [x(1)^2 + x(2)^2 - 1; x(1) - x(2)], [0; 0])2. Mathematica
Mathematica est un autre outil robuste qui permet de résoudre symboliquement et numériquement des systèmes d’équations non linéaires. Sa fonction NSolve est particulièrement efficace :
NSolve{x^2 + y^2 == 1, x - y == 0, {x, y}}3. Python avec SciPy
Pour les développeurs et les passionnés de programmation, Python offre des bibliothèques comme SciPy qui inclut la fonction fsolve pour la résolution de ces systèmes :
from scipy.optimize import fsolve
fsolve(lambda x: [x[0]2 + x[1]2 - 1, x[0] - x[1]], [0, 0])4. R
Le langage R est également utilisé pour résoudre des systèmes d’équations grâce à des packages tels que nleqslv. Voici un exemple :
library(nleqslv)
nleqslv(c(0, 0), function(x) c(x[1]^2 + x[2]^2 - 1, x[1] - x[2]))Tableau comparatif des logiciels
| Logiciel | Langage | Fonctionnalité principale |
|---|---|---|
| MATLAB | Propriétaire | fsolve |
| Mathematica | Propriétaire | NSolve |
| Python (SciPy) | Open source | fsolve |
| R | Open source | nleqslv |
Conseils pratiques pour l’utilisation de ces outils
- Choisissez le bon outil : Selon vos besoins, certains logiciels peuvent offrir des fonctionnalités plus adaptées.
- Utilisez des exemples concrets : Tester vos systèmes d’équations avec des exemples connus peut valider la précision de vos solutions.
- Explorez la documentation : Prenez le temps de lire la documentation des outils pour découvrir toutes leurs fonctionnalités.
En fin de compte, l’utilisation de ces logiciels et outils peut grandement simplifier le processus de résolution des systèmes d’équations non linéaires, rendant le travail mathématique plus accessible et efficace.
Questions fréquemment posées
Qu’est-ce qu’un système d’équations non linéaires ?
Un système d’équations non linéaires est un ensemble d’équations où au moins une des équations n’est pas linéaire. Elles peuvent inclure des polynômes, des exponentielles, des logarithmes, etc.
Comment résoudre un système non linéaire ?
Les systèmes non linéaires peuvent être résolus par diverses méthodes comme la substitution, l’élimination, ou des techniques numériques comme la méthode de Newton-Raphson.
Quelles sont les applications des systèmes non linéaires ?
Ces systèmes sont utilisés dans de nombreux domaines tels que la physique, l’économie, et l’ingénierie pour modéliser des phénomènes complexes.
Quels outils utiliser pour résoudre ces systèmes ?
Des outils comme MATLAB, Mathematica ou Python avec des bibliothèques telles que NumPy et SciPy facilitent la résolution de systèmes d’équations non linéaires.
Quels sont les défis courants ?
Les défis incluent la multiplicité des solutions, la convergence des méthodes numériques, et la sensibilité des solutions aux variations des paramètres.
Points clés sur la résolution des systèmes d’équations non linéaires
- Identification des types d’équations : polynomiales, exponentielles, etc.
- Choix de la méthode de résolution : analytique ou numérique.
- Utilisation d’outils logiciels pour faciliter la résolution.
- Analyse de la solution : vérifier l’existence et l’unicité.
Nous vous invitons à laisser vos commentaires et à consulter d’autres articles sur notre site Internet qui pourraient également vous intéresser !